Senior Physics Challenge Day 2

I'm writing this at quarter to eleven at night, so this is your fault dear reader, if I am late to breakfast at 8:15 tomorrow morning.

The short version of my day is wrapped up nicely by my timetable: breakfast at Corpus Christi from 8 to 8:30. Leave to go to Cavendish Labs by 9:00. Classical mechanics lecture from 9:15 to 10:30 and then a short break before a quantum mechanics lecture that ended at around 12:30 and after that we ate lunch. Starting at 13:30 I had labs, with the topic for today being a conical pendulum question that was very interesting. After labs (which were 2 hours by the way), we went punting and then at 7 O'clock we had an admissions talk and Q&A which I won't describe here because most of the stuff is available on their website to be honest, or just ask on TSR.

Classical mechanics was not particularly enlightening to be honest, the highlight was the epitaph of Stevinus, which would have been far more exciting if it hadn't been included in chapter 4 of Volume I of the Feynman lectures. Nevertheless, some problems were quite interesting and they were more conceptually involved than mathemetically which is how I like my mechanics problems.

Quantum mechanics was perhaps the day's highlight - we got to cover the foundational postulates of quantum mechanics, which are:

(Postulates of quantum mechanics)

The state of a system is completely determined by the wavefunction, w(x). In general w is actually a complex function of up to four variables, w=w(x,y,z,t). The wavefunction encodes all imformation possible about the system, there is no need to know anything else.
The probability density at a given point, p(x) is given by the norm squared of w(x). For real valued w(x), this jut means squaring w(x). Probability density is the probility of finding the particle per unit length at that spot, so the probability of finding a particle between a point x and (x+dx) is p(x)dx = w2(x)dx
To every observable there is an associated operator which is linear. Operators are like functions of functions, they take one function and output a new function. The simplest example might be the derivative operator - it takes f(x)=x^2 and outputs a new function f'(x)=2x. In quantum mechanics all observables have associated operators which are given hats (^) to denote their status. For these blog posts I'm going to use the following notation: {O} to denote an operator.
The result of a measurement will be an eigenvalue of the associated quantum operator. This needs explaining.

The operator {d/dx} can act on many functions. In general it will act in this way:

{d/dx}f(x) = g(x)

However, with one particular function, the exponential, it acts in this way:

{d/dx}f(x)=af(x)

Instead of producing a new function, it just reproduces the old, but with a scalar constant in front. The exponential is an 'eigenfunction' of {d/dx} (eigen just means 'same'), and 'a' is an 'eigenvalue' of {d/dx}. When you take a measurement of energy, the only possible energies are the eigenvalues of the energy operator. So, what's the energy operator?

In general, all we know is that {E}={T}+{U}, where T is the kinetic energy operator and {U} is the potential energy operator. But {T} is always the same: {T} = {-hbar^2/2m * d2/dx2}, and in the case of a zero potential we have U = 0. So in free space, you have {E} = {T}.

Now we use the fourth postulate to say that the energy of a particle must be an eigenvale of the {E} operator acting on w(x), giving us the Schroedinger equation:

-hbar^2/2m * (d2/dx2)w(x) = Ew(x)

rewriting that a little gives w''(x) = -2mE/hbar^2 w(x)

This is exactly the same differential equation as for simple harmonic motion, with the solution being sines and cosines with wavenumber of sqrt(2mE/hbar^2). If you use complex numbers and let -2mE/hbar^2 = k^2, then you can solve this analytically quite easily to get a complex exponential, which is the same as a sine wave.

The last thing which I have time to write about is labs - we were given two hours to time the length of time for a pendulum bod wrapped around pieces of dowel of different thicknesses to unwrap different numbers of windings. This required two experiments: one to find the dependence of the number of windings and one for the diameter of the dowel. First up, we threaded the pendulum string through a hole in the dowel and wrapped it around, then repeated for different numbers of windings.

Our results were... not too good. We had trouble getting the pendulum to actually unwind and swing in a conical path rather that, you know... just falling to the floor. The data we did get looked like this:

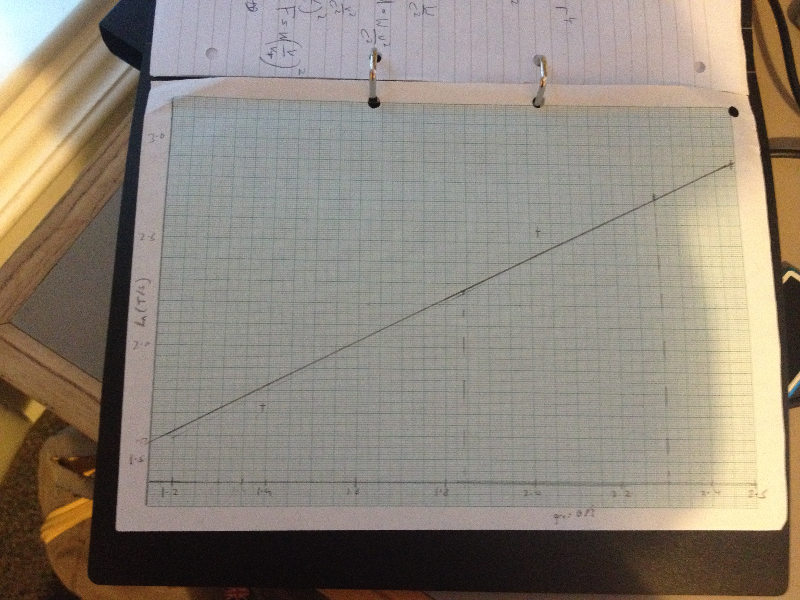
(ln/ln graph of t vs n. The points are plotted with error bars which are slightly tricky on log scales (you work where they would be on linear scales and take the logs of those positions) and a line of best fitted drawn on. You can tell the data was pretty awful because the line of best fit cannot possibly go through our error bars.)

The experimental analysis ran like this: assume T = k n^a d^b , where n is number of windings, d is diameter etc.

Then for a fixed diameter ln(T) = ln(kd^b) + aln(n). Plot of graph of ln(T) vs ln(n) and read off the gradient. Do the same for the second experiment to find b, then use the two y intercepts to solve for k. Additionally, we had to plot error bars and calculate the standard deviation in all or our readings. The theoretical analysis runs more like this:

Let the total angle that the pendulum has turned through be A - this can be larger than 2pi as the pendulum spins multiple windings. The length of the pendulum at any given time is l=rA, where r is the radius of the dowel. Resolving vertically and horizontally for the pendulum, you should come to the conclusion that (d/dt)(A) = sqrt(g cos(theta) / l). This gives you a first order seperable differential equation in A, namely A' = sqrt(g cos(thet)/r) A^(-0.5)

Seperating variables and integrating gives you:

Int(0 to nTao)[A^0.5]dA = Int(0 to T)[sqrt(g cos/r)]dt

2(nTao)^(3/2)/3 = Tsqrt(g cos / r)

You could solve for T, but Wix is annoying at times like these, so I'll just hope that you can see that T depends on n such that a=1.5 and on d such that b=0.5.

*Phew* that was a lot of work today. Luckily we pretty much finished by 3 and then just messed around for the rest of the day! Same again tomorrow.