Senior Physics Challenge Day 1
- aspiringphysicist
- Jun 29, 2015
- 5 min read
Today was the first day of the Senior Physics Challenge hosted by Cambridge University and we didn't do too much today as it was more of a welcome day than anything else. I turned up at Corpus Christi College at about half four, and went to get the keys for my accommodation - accommodation which they had apparently rented out, and so those staying at Corpus are actually staying 5-10 minutes down the road (not that that's a problem, but Corpus looks lovely and it would be nice to be staying actually in a college for these four nights).

(Picture of my room and some of my things.)
After a brief tour of the university, we ate dinner (which was very nice), were told what times to turn up for breakfast and at Cavendish Labs tomorrow morning and then we went off to do the evening's recreation: 'physics estimation'. Now, obviously that does sound a little nerdy to do that for fun, but as it turns out, it was actually a lot nerdy. But also lots of fun. We split into teams of five, and had about fifteen to twenty minutes (I think)to estimate seven physical quantities:
The rate of mass loss of the Sun (due to energy production)
The radius of a black hole with the Earth's mass
The area needed to be covered with solar cells to replace current UK electric power requirements
The ratio of the drag force to the weight force acting on a tennis ball just after a professional serve
The mechanical power of the human heart
The drift speed of electrons powering an LED room lamp
The ionization energy of a Hydrogen atom

We were also given a list of some numbers including fundamental constants such as Planck's constant and Boltzmann's constant (also the mass of the Earth and the total solar flux on the Earth amongst other things). We were however, told that this was cheating and was really only being allowed because we were newbies.
So, how to approach these questions? I'll list the ways that my group tried to use, although we didn't always estimate the relevant quantities correctly.
1) This one was fairly simple - if the flux on the Earth is 1.4kW/m2 then the total flux through a sphere of radius 1AU is just 4pi*(1.4e3)*(1.5e8)^2. Divide that through by c2 for an energy loss expressed in kgs-1. I won't bore you with the calculation, but without calculators it involves quite a lot of rounding.
2) This is an interesting problem in and of itself, the key idea is that the escape velocity of a black hole is the speed of light (or greater). The escape velocity is the velocity such that your kinetic energy equals your potential energy at that point, so
mv^2 = 2mMG/r
substituting v=c and solving for r you get:
r=2MGc^(-2)
which calculated gives about 1cm.
3) The area of solar panels needed to power the UK. This was a difficult one as there were many confounding factors: flux is 1.4kW/m2 but solar panels are not 100% efficient. In fact, you lose a factor of 2 for night time, in the UK you probably lose another factor of 2 for cloud cover and a third for latitude. Then you have the fact that solar panels are only maybe 20% efficient so you're talking maybe 35W/m2. Estimating the UK's power usage at around 30GW gives just under 109m2of solar panels.
4) The ratio of the drag force to the weight on a tennis ball. There were lots of numerical approaches here with estimations of court length, serve speed, landing velocity et cetera. My favourite method is actually the following though:
Assume that the drag force is proportional to velocity squared, hence F=bv2. If you dropped that tennis ball from a tower, it would hit a terminal velocity c, such that b=W/c2, where W is the weight of the ball. So now, the drag force on the tennis ball is given by:
F = W(v/c)^2
Hence the ratio we want is just (v/c)^2. Unfortunately, whilst we could guess at 100mph for a serve velocity, nobody had a good estimate for a tennis ball terminal velocity, so I suggested we just put the answer 10 as approximately correct (this was confirmed as being in the right ballpark).
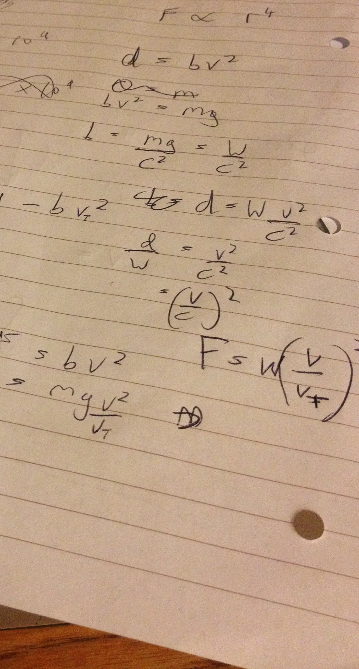
(My working on paper is probably more legible for the tennis ball question. Which is saying something, because I appear to follow no logical sequence and have the same result four times on a single sheet of paper).
5) The mechanical power of the human heart - this is an interesting one. We went about this in completely the wrong way, trying to work out the energy needed to lift 3L of blood about 2m and work back from there. A much better way was suggested, which was that typical blood pressure is "120 over 80": in other words, the pressure of blood leaving the heart is around 120mmHg 1atm = 760mmHg = 101kPa, so 120mmHg is 16kPa. Blood flowing through the heart has to travel about 10 cm in half a second giving it a velocity around 0.2m/s and the cross section of the aorta is probably around 5e-4m2 multiplying that all out gives you 1.6W. The correct answer is apparently around 6W, so that's not bad.
6) The drift speed of electrons powering an LED lamp. The lamp will be connected to mains voltage and have a power output somewhere around 5W giving a current of ~0.02A. Then using I =nAvq
We can rearrange for v: v= I/(nAe)
or (0.02) / [(1028 *10-5 *10-19 ] ~ 10-6m/s.
7) Ah, calculating the Rhydberg constant. We did actually know the correct value at 13.6eV. One of us tried to calculate that by working out the difference between the mass of a proton and of a Hydrogen atom, then take the difference and convert it to a mass via E=mc2. That didn't work though, because unsurprisingly the mass of a proton and the mass of a Hydrogen atom cancel out unless you use ridiculously precise numbers.
A more fruitful method might have been to try to use the actual definition:
Ionisation energy = work done to bring charge to infinity
=Int(r,infty) [kqQ/r^2 ] dr
=ke^2/r
where r is the Bohr radius which is approximately half an Angstrom (5e-11) and k is Coulomb's constant. To get the answer is electron volts you just drop a factor of e to get E=ke/r.
Typing that into a calculator right now gives me 29eV. Unfortunately, I didn't know the value for Coulomb's constant at the time, so that went badly.
But wait! If the correct calculated value is 29eV, why did I start by saying it was 13.6eV? It turns out that the classical calculation is flawed and that the correct value of the ionisation energy for Hydrogen can only be obtained using Quantum Mechanics.
Looking forwards to the next four days, I have labs tomorrow morning!
(Sidenote: we really didn't do very much today, I've just span this post out an awful lot. Do not expect so much detail over the next couple of days because I imagine it will be close to impossible!)















Comments