Difficult Solutions
Copper is three times as dense as aluminium, and has half the resistivity- what is the ratio between the mass of two equal lengths of copper and aluminium if they have the same resistance?
So, a more physics based post this time around I hope! I want to focus on how to solve difficult problems- problems that are outside the usual and need a little more thought than some of the "plug-and-chug" style questions that A level physics is sometimes a little too full of.
So, before we begin I want to make two analogies: the first is a cereal box puzzle. Kelloggs make multi-pack cereals, but they never remember to change the puzzles. So the answer to the puzzle on the back of the 'coco pops' box is "B" and has been for years. The first thing to learn from this is you can be overfamiliar with content.
The second, is how you can tell it's B. You have to tell which of three paths go to the final destination- a lovely bowl of chocolate cereal! Simple, right? Just follow each of the paths in turn, until you find the correct one. Well, not unless you want to check all three paths. A difficult physics problem might have twenty different 'routes'. The fastest and therefore optimal solution is to simply start at the bowl where there is only one path and trace it back. So the lesson is this: you can start from the front and work forwards OR you can start from the back and work backwards. Both work, but one is sometimes better than the other.
The next example I thought of occurred today in my Core Maths lesson on sequences. The sequence was:
26 , 14, 8, 5, 7/2
What was the first thing I did? Looked at the differences: -12, -6,-3 etc
So I'd noticed a pattern. I then diligently wrote out the pattern in maths-speak:
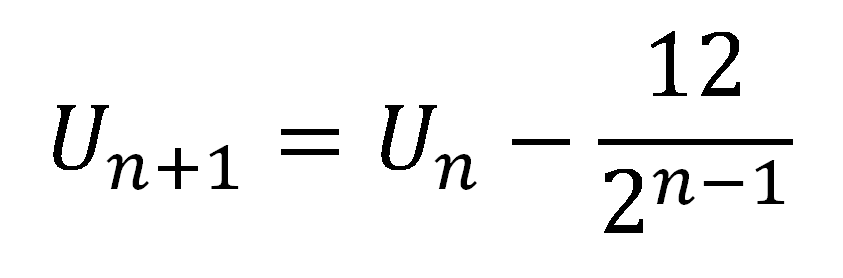
Which should have rung alarm bells. The pattern I had noticed was that every term along, the difference halved. The above does genuinely output the correct sequence, I'm pretty sure. But it is ugly, and clearly not the intended answer.
My friend then told me to halve each term, and add one. Which was much nicer.
So: good solutions are elegant, and not messy. And you can sometimes help a solution along by starting at the finish.
With that in mind, let's move onto the question at hand: if copper is three times as dense as aluminium, and has half the resistivity- what is the ratio between the mass of two equal lengths of copper and aluminium if they have the same resistance?
Now, to be fair, I did manage to get a reasonably pretty answer to this using my initial method (which was to solve for the ratio of their cross sectional areas using the resistivity equation and then to use this to determine the ratio of the masses, alongside their densities.)
But there is a simpler way to conceptualise the question:
Start with the answer. Let the ratio between their two masses =(mass of copper)/(mass of aluminium).
Then write in the formula for mass- mass=density X volume
Rewrite copper's density in terms of aluminium using the information in the question, and cancel the terms.
=3(volume of copper)/(volume of aluminium)
You know the length is constant, so really you just need cross sectional area:
=3(area of copper)/(area of aluminium)
Which, given that resistance and lengths are constant, is inversely proportional to resistivity:
=3(resistivity of aluminium)/(resistivity of copper)
(N.B. the fraction is flipped because cross sectional area is inversely proportional to resistivity
Rewrite one resistivity in terms of the other, cancel and you're left with 3/2. Done









